621
Physics Rotational Mechanics Level: High School
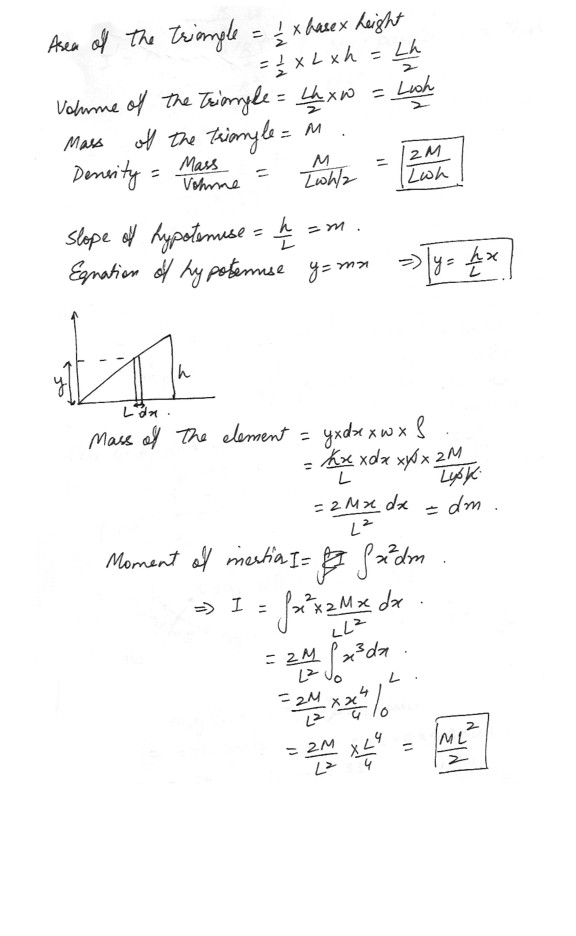
Calculate the moment of inertia of a thin plate, in the shape of a right triangle as shown in the figure at “click here” . Let M represents the mass of the triangle and L the length of the base of the triangle perpendicular to the axis of rotation . Let h represent the height of the triangle and w(omega) the thickness of the plate , much smaller than L or h. Use the integral form of the moment of inertia equation . Let an element of mass consist of a vertical ribbon within the triangle , of width dx , height y, and thickness w . With x representing the location of the ribbon, show that y = hx/L . Show that the density of material is given by p=2M/L wh . Show that the mass of the ribbon is dM = pywdx = 2Mxdx/L^2 . Then calculate the moment of inertia from the integral equation .