Mathematics Integration Level: Misc Level
What are standard integrals and integrals of trignometric functions?

Mathematics Integration Level: Misc Level
What are standard integrals and integrals of trignometric functions?

Mathematics Integration Level: Misc Level
What are the fundamental notations of integral calculus, properties of definite integrals and solutions of differential equations?

Mathematics Integration Level: Misc Level
What are the fundamental notations of integral calculus, properties of definite integrals and solutions of differential equations?

Mathematics Integration Level: Misc Level
For f (x)=x^2 (5-7x^3)^4 find integral of f(x)
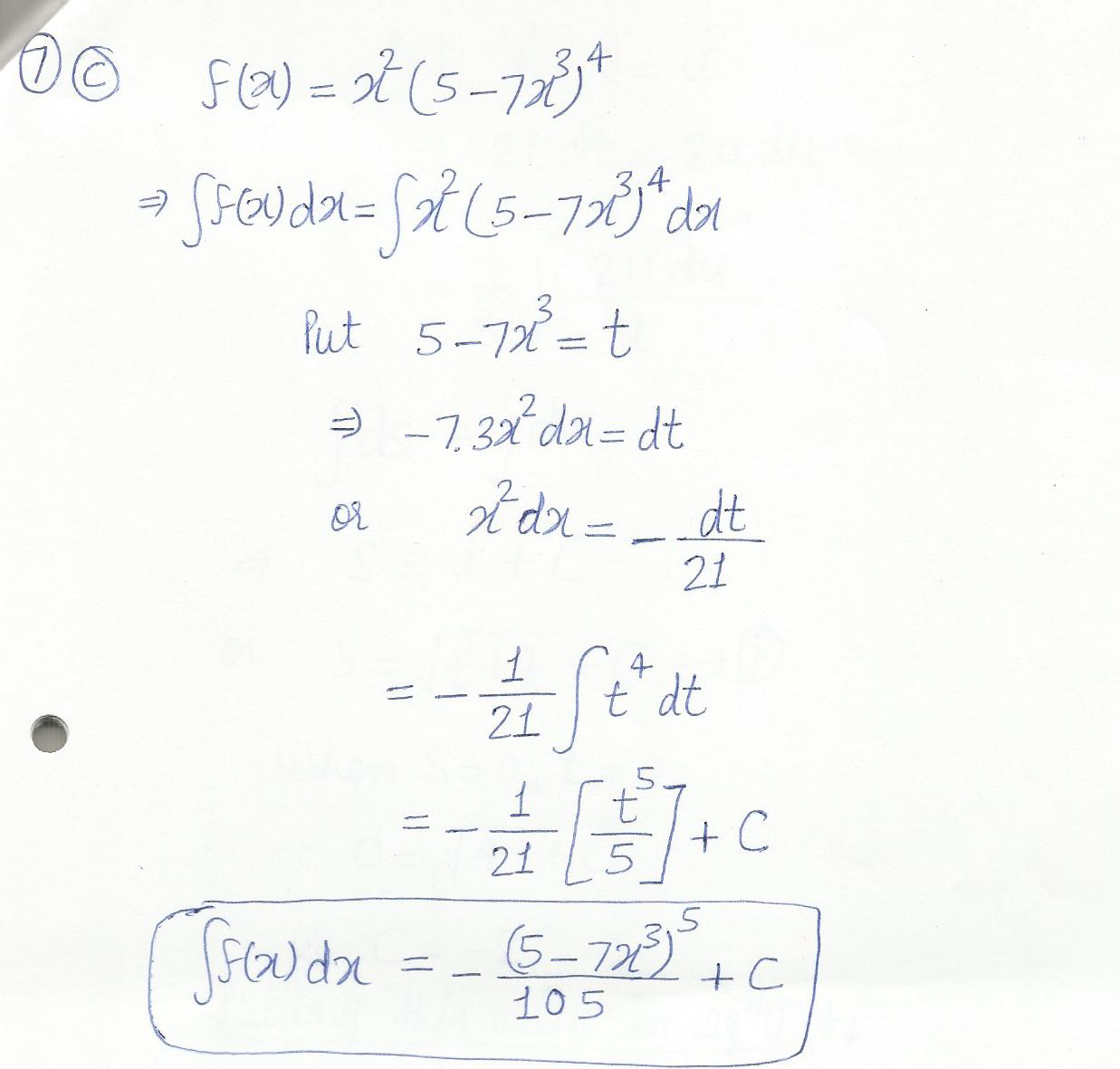
Mathematics Integration Level: Misc Level
An open box with a square base is to be made out of a given quantity of cardboard whose area is c2 square units. Show that the maximum volume of the box is cubic units.
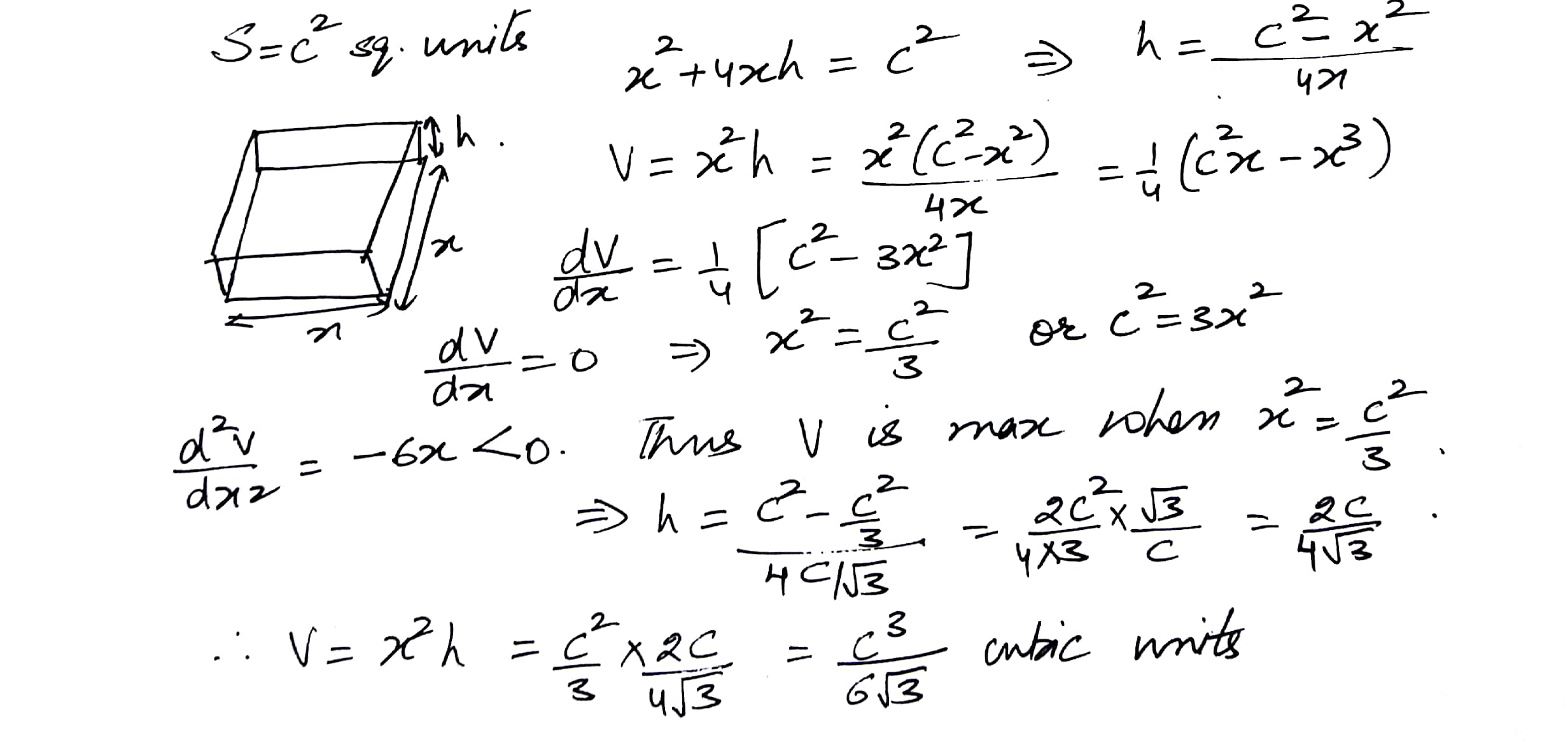
Mathematics Integration Level: Misc Level
Show that the semi-vertical angle of the right circular cone of given total surface area and maximum volume is

Mathematics Integration Level: Misc Level
Find the maximum volume of the cylinder which can be insrcribed in a sphere of radius cm. (Leave the answer in terms of
)

Mathematics Integration Level: Misc Level
A closed right circular cylinder has a volume of 2156 cubic cm. What will be the radius of its base so that its total surface area is minimum? Find the height of the cylinder when its total surface is minimum. Take =22/7
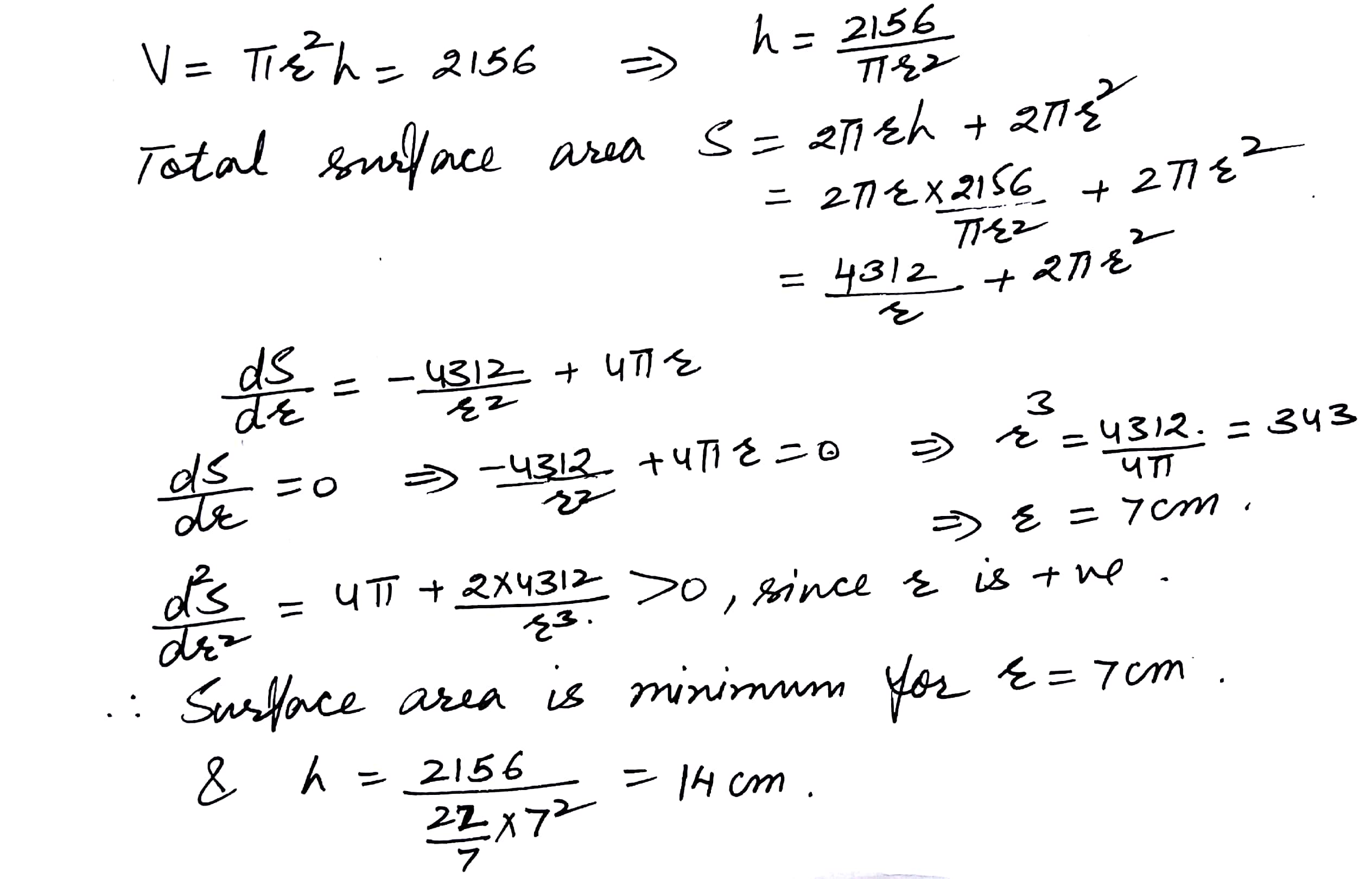
Mathematics Integration Level: Misc Level
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top by cutting off squares from the corners and folding up the flaps. What should be the side of the square in order that the volume of the box is maximum?

Mathematics Integration Level: Misc Level
An open box with a square base is to be made of given iron sheet of area 27 square meters. Show that the maximum volume of the box is 13.5 cubic meter.

Mathematics Integration Level: Misc Level
Show that the surface area of a closed cuboid with square base and given volume is minimum when it is a cube
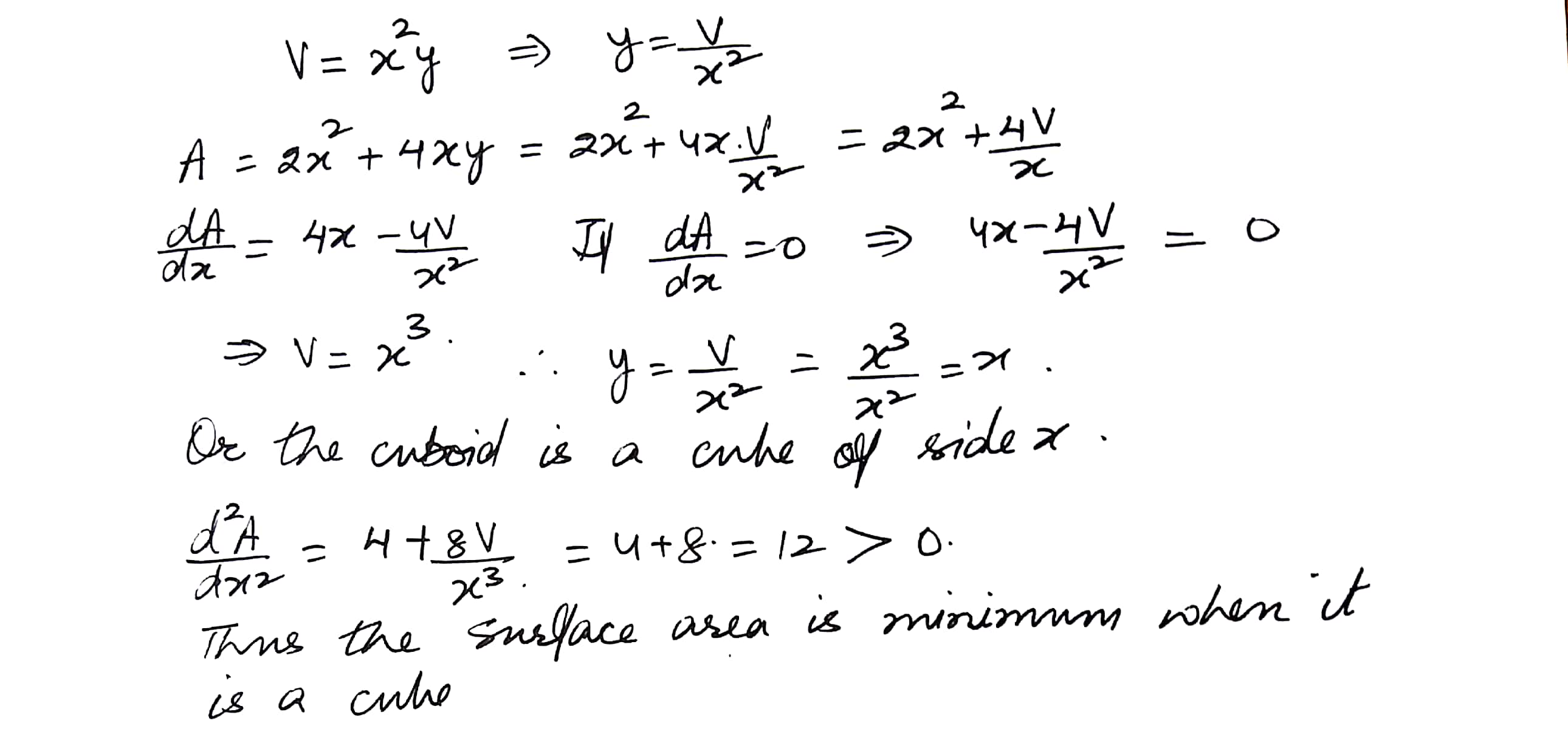
Mathematics Integration Level: Misc Level
Find the point on the parabola y2 = 4x which is nearest to the point (2,-8)

Mathematics Integration Level: Misc Level
A window is in the form of a rectangle above which there is a semicircle. If the perimeter of the window is p cm, show that the window will admit maximum possible light only when the radius of semicircle is cm
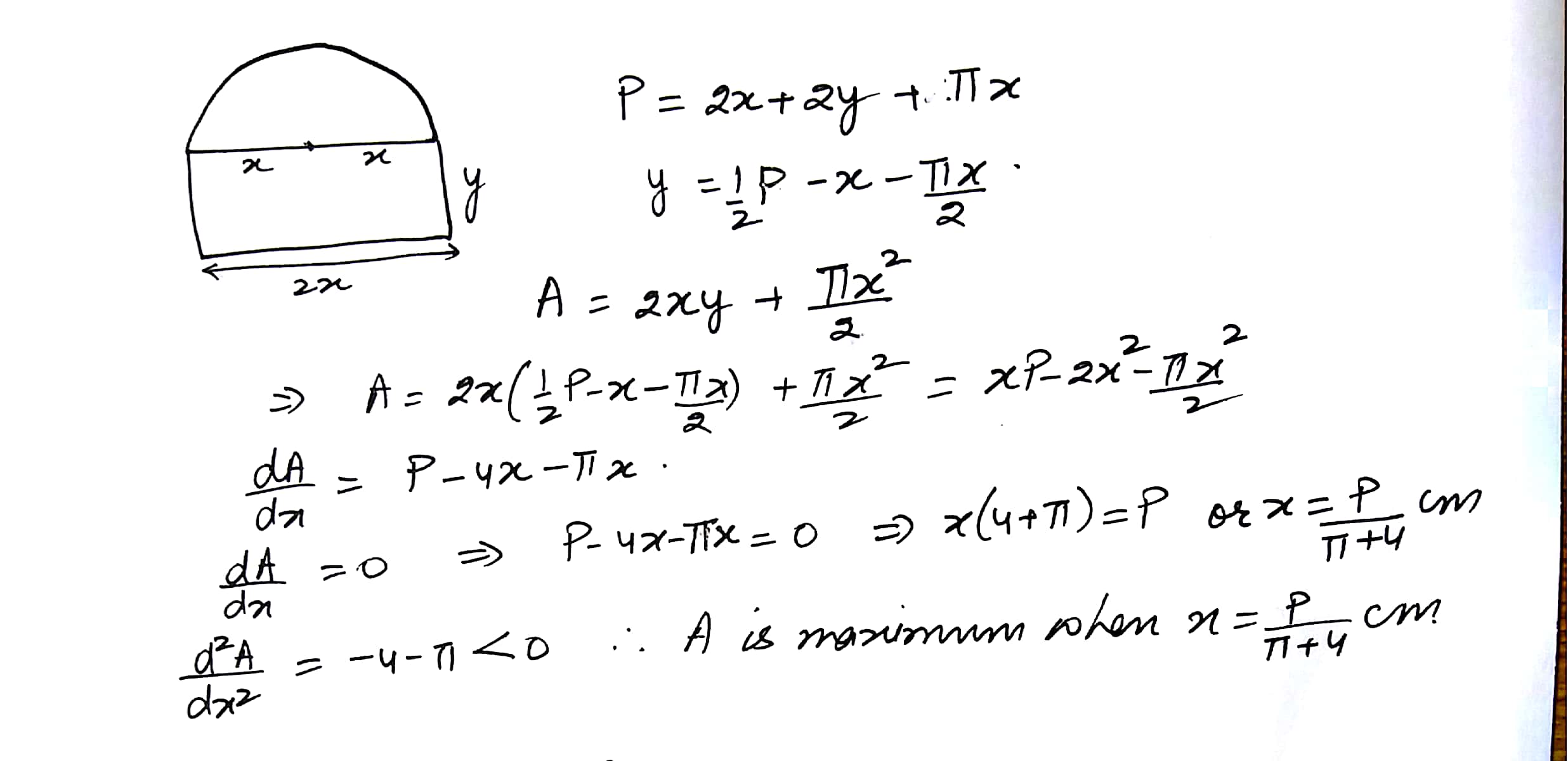
Mathematics Integration Level: Misc Level
A wire 10 meters long is cut into two parts. One part is bent into the shape of a circle and the other into the shape of an equilateral triangle. How should the wire be cut so that the combined area of the two figures is as small as possible?

