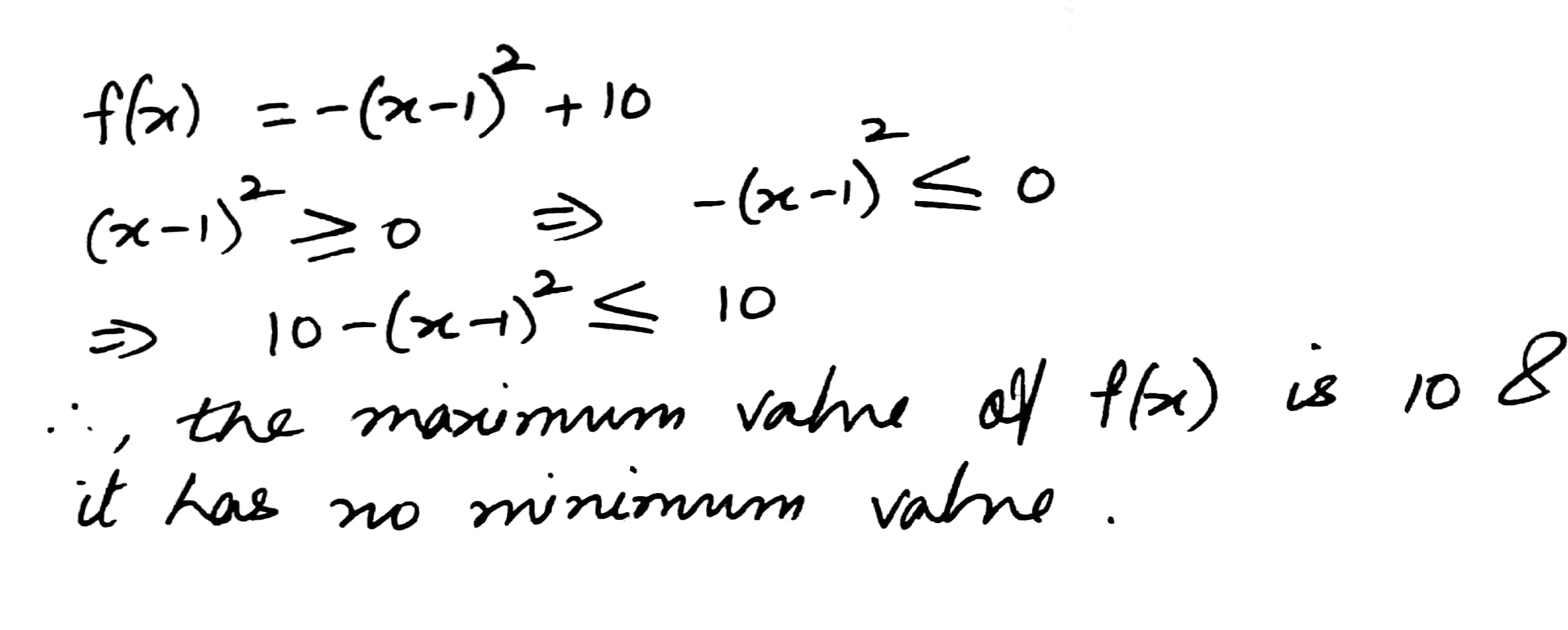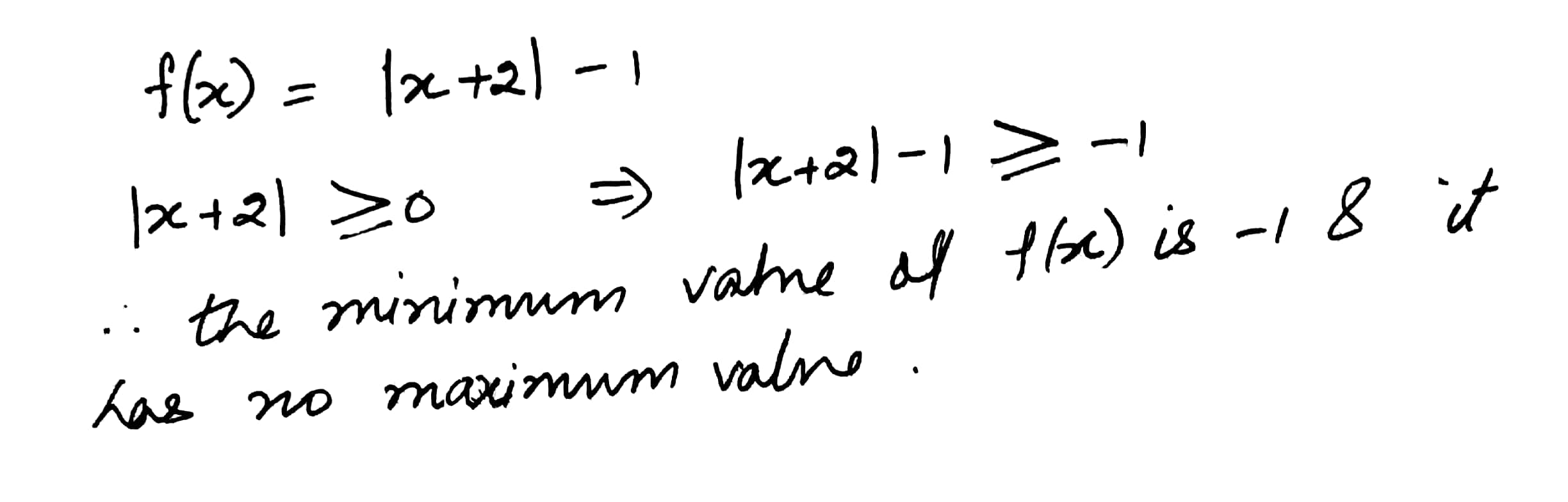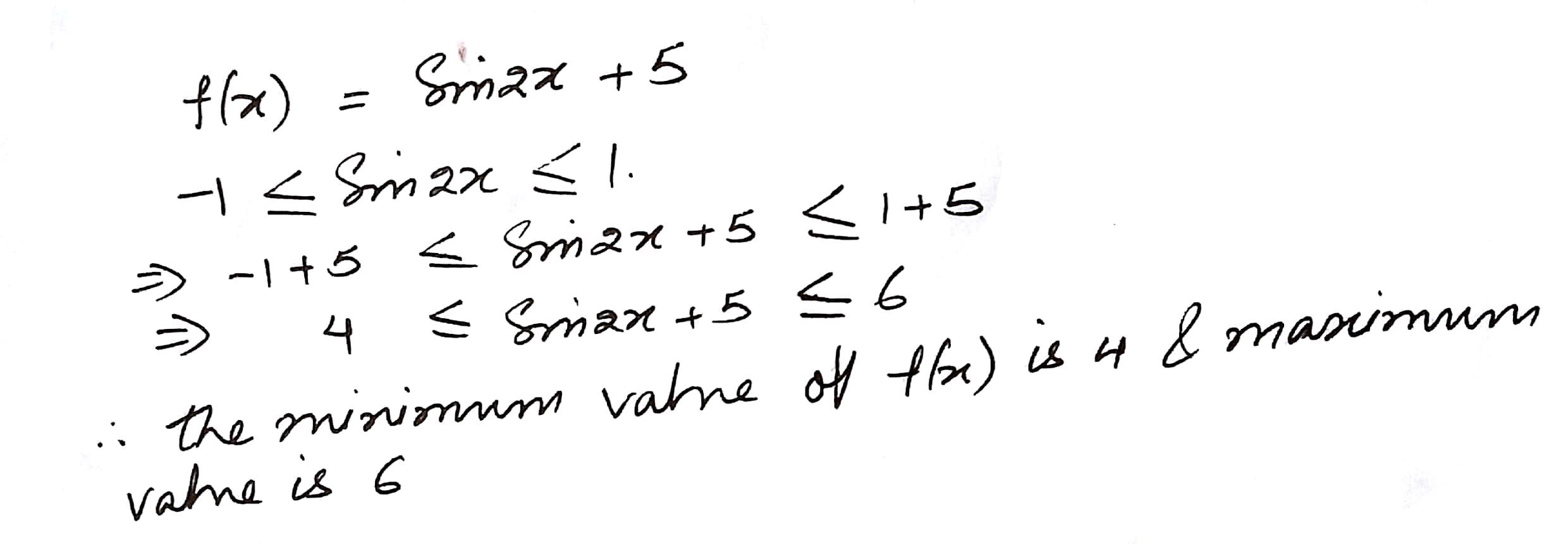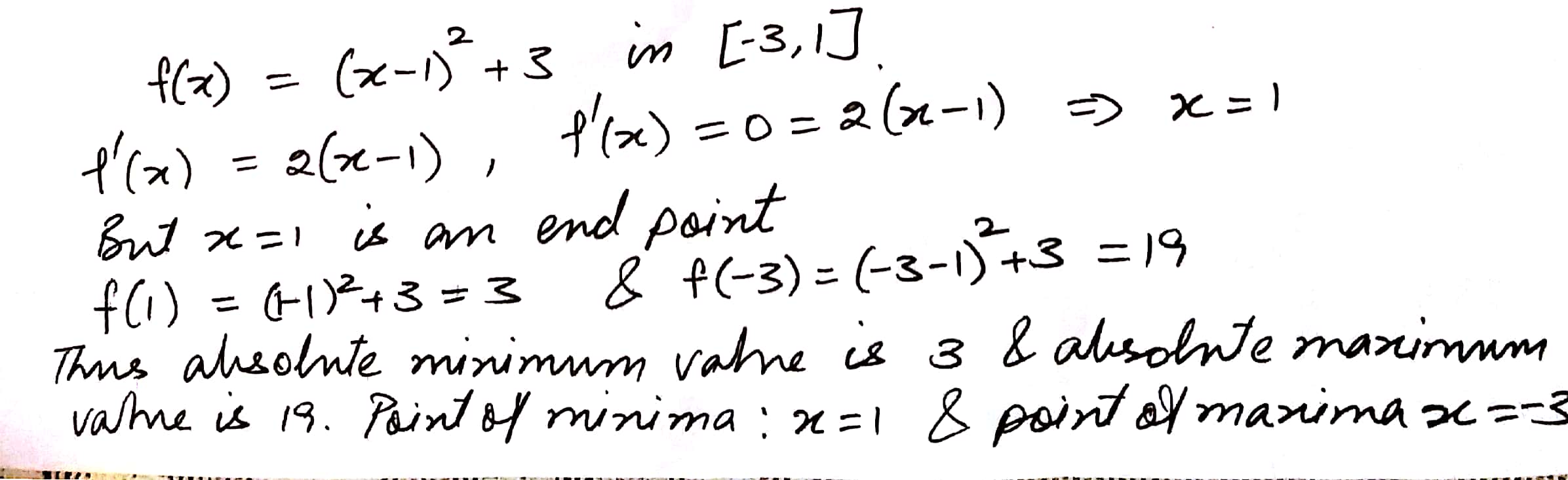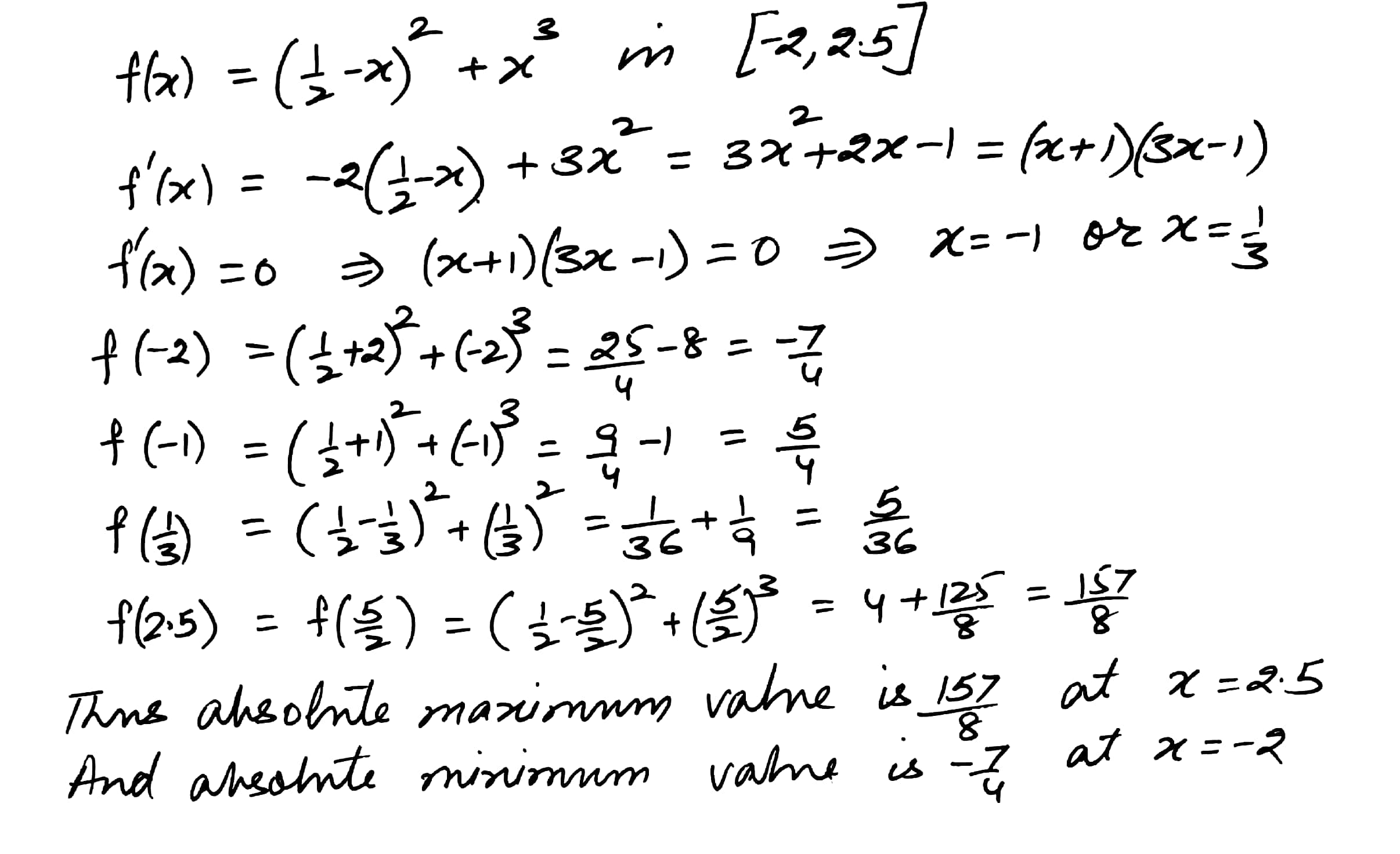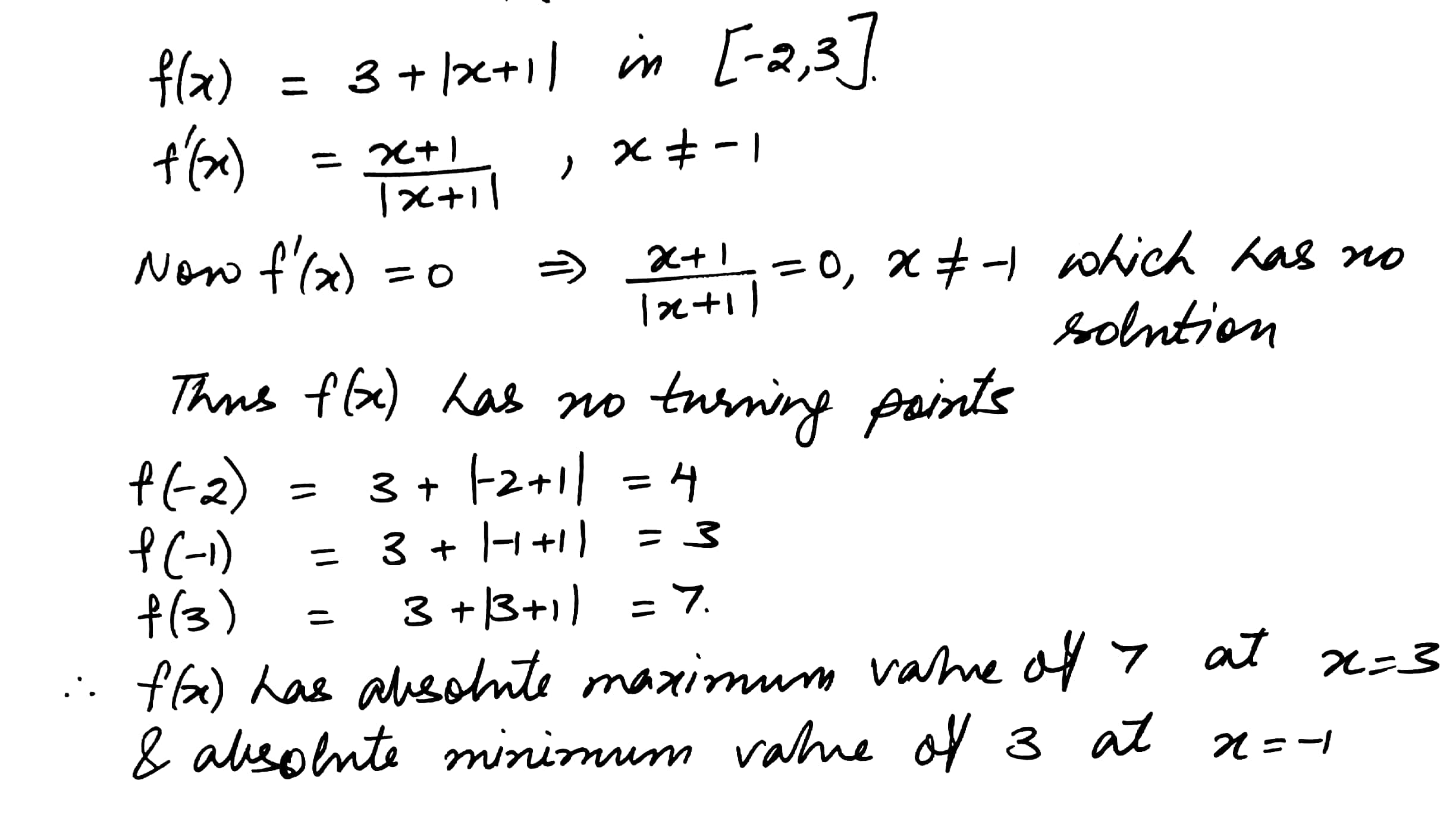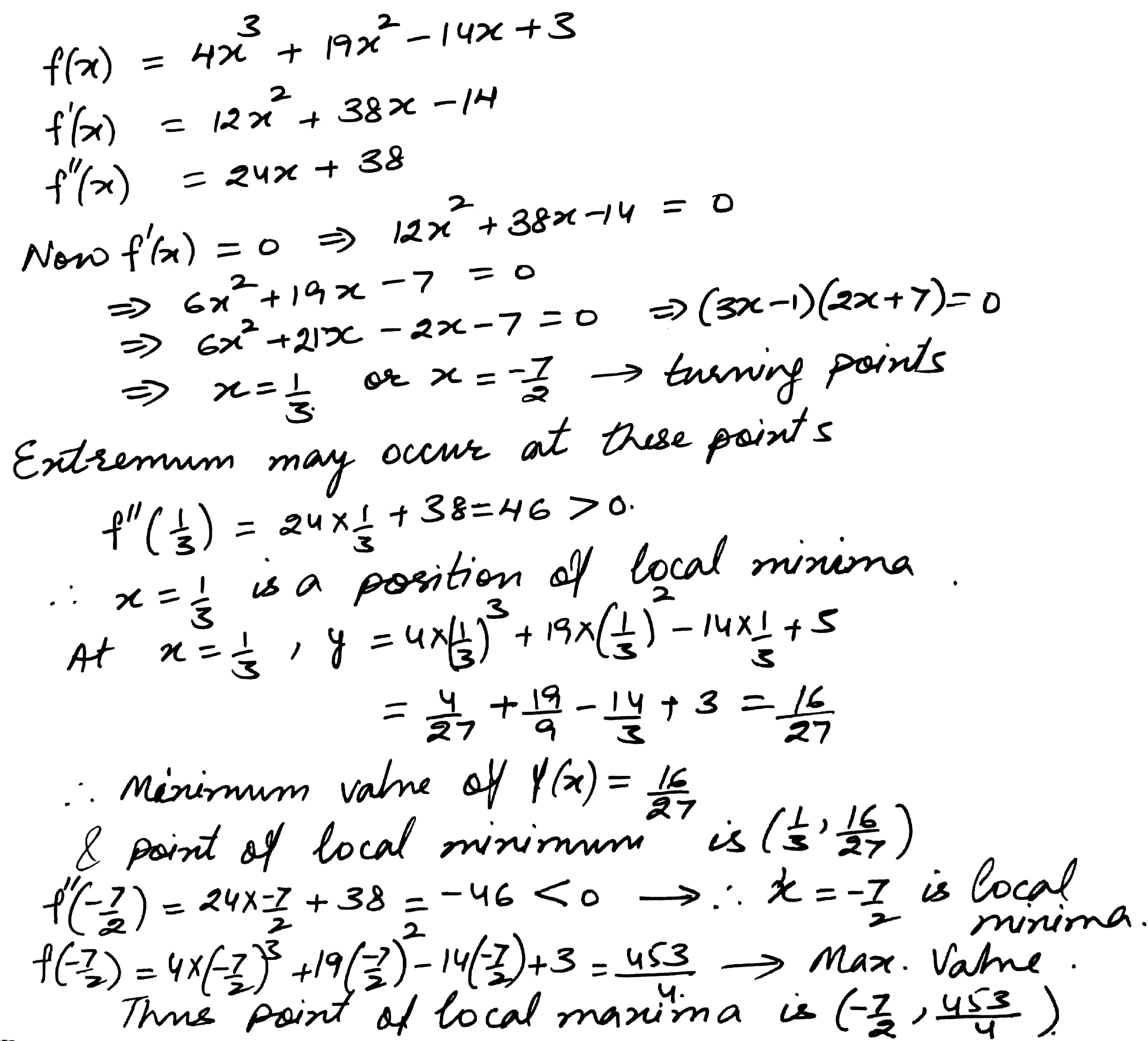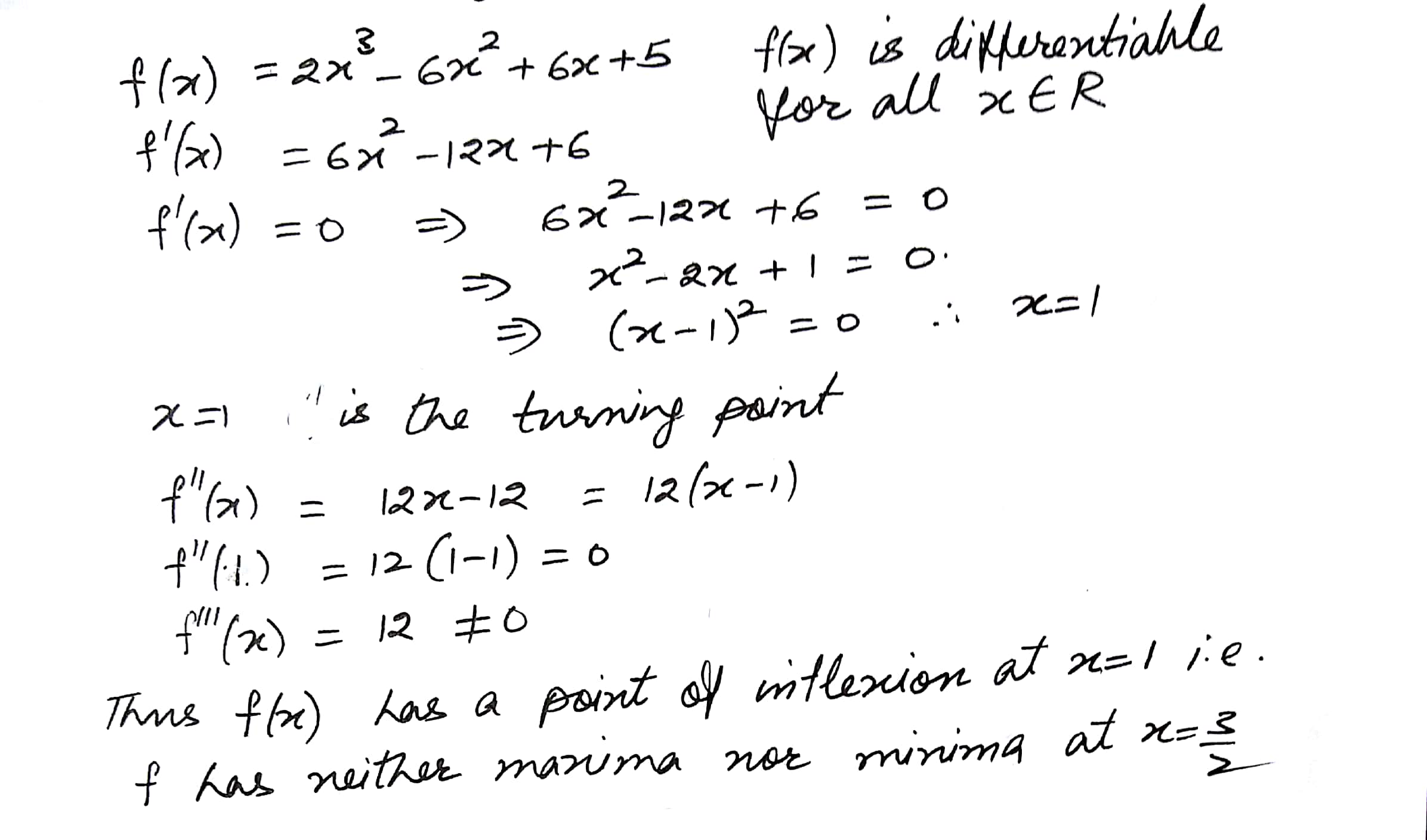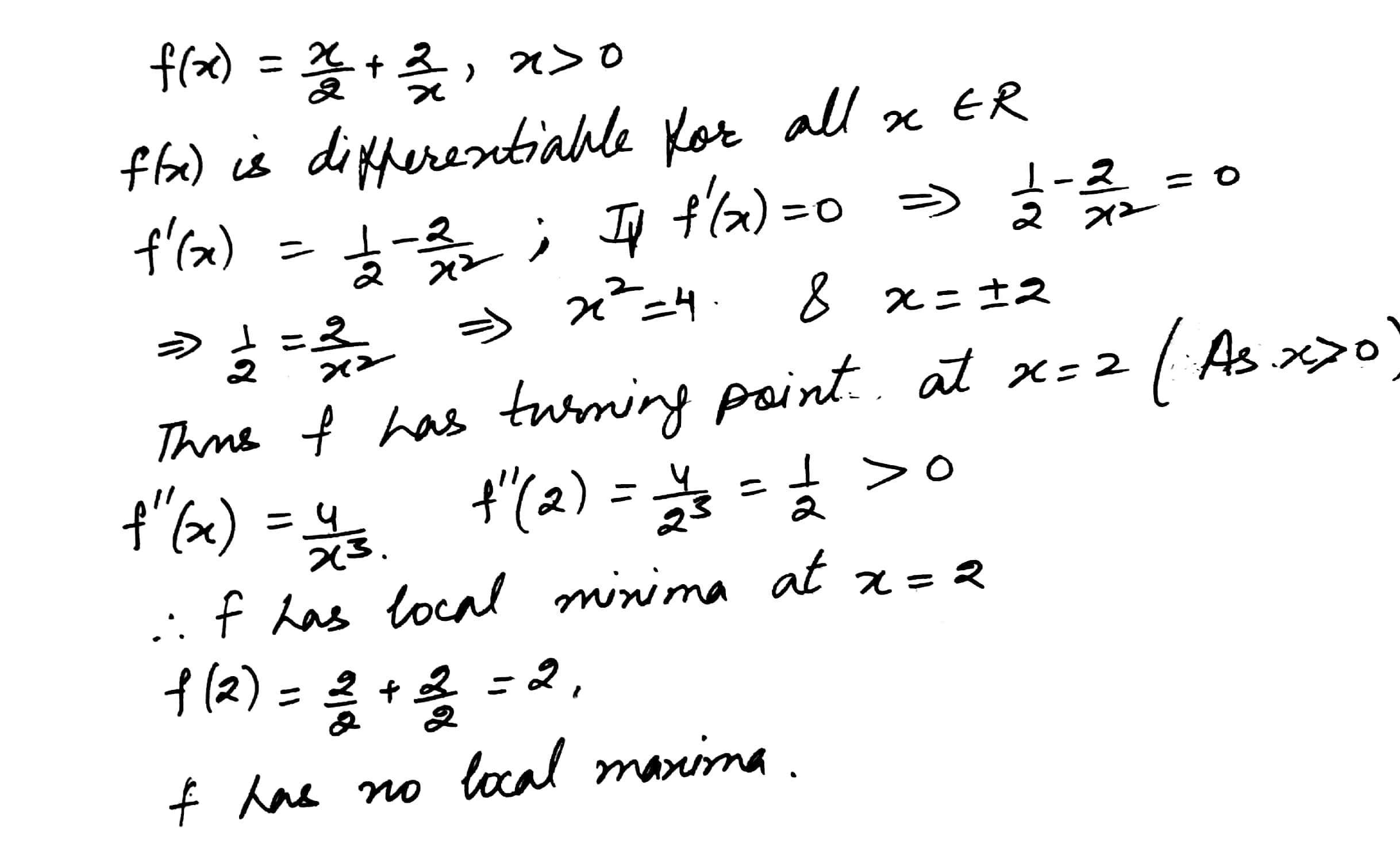Mathematics Integration Level: Misc Level

Find the maximum and the minimum values (if any) of the following function

f(x) = - (x-1)² + 10

Mathematics Integration Level: Misc Level

Find the maximum and the minimum values (if any) of the following function

f(x) = |x + 2| - 1

Mathematics Integration Level: Misc Level

Find the maximum and the minimum values (if any) of the following function 

f(x) = Sin 2x + 5

Mathematics Integration Level: Misc Level

Find the (absolute) maximum and the (absolute) minimum values of the following function in the indicated intervals. Also find the points of (absolute) maxima and minima

f(x) = (x-1)² + 3 in [-3,1]

Mathematics Integration Level: Misc Level

Find the (absolute) maximum and the (absolute) minimum values of the following function in the indicated intervals. Also find the points of (absolute) maxima and minima

Mathematics Integration Level: Misc Level

Find the (absolute) maximum and the (absolute) minimum values of the following function in the indicated intervals. Also find the points of (absolute) maxima and minima

f(x) = Sin x + Cos x in [0,]

Mathematics Integration Level: Misc Level

Find the (absolute) maximum and the (absolute) minimum values of the following function in the indicated intervals. Also find the points of (absolute) maxima and minima

f(x) = 3 + |x+1| in [-2,3]

Mathematics Integration Level: Misc Level

Find the turning points of function f(x) = 4x³ + 19x² - 14x + 3 amd distinguish between them. Also find the local maximum and the minimum values of the function.

Mathematics Integration Level: Misc Level

Find the points of local maxima and minima (if any) of the following function. Also find the local maxima and minima values

f(x) = 2x³ -6x² + 6x + 5

Mathematics Integration Level: Misc Level

Find the points of local maxima and minima (if any) of the following function. Also find the local maxima and minima values