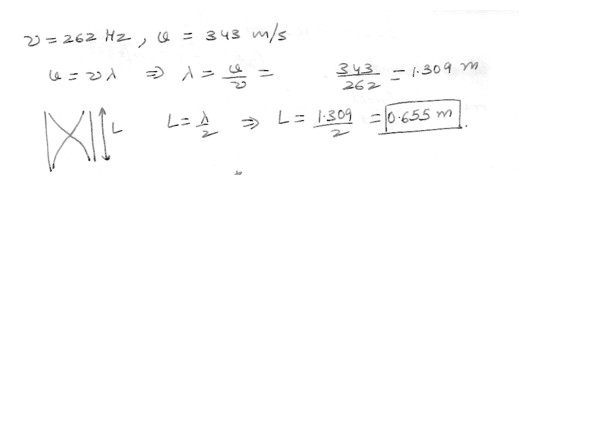Physics Waves And Oscillations Level: High School
Sound
Many artists sing very high notes in ab lib ornaments and cadenzas .The highest note written for a singer in a published score was F-sharp above high C , 480 kHz ,sung by Zerbinetta in the original version of Richard Strauss’s opera Ariadne auf Naxos .A) Find the wavelength of this sound in air .
B) In resonance to complaints , Strauss later transported the note down to F above high C ,1.397 kHz . By what increment did the wavelength change ?
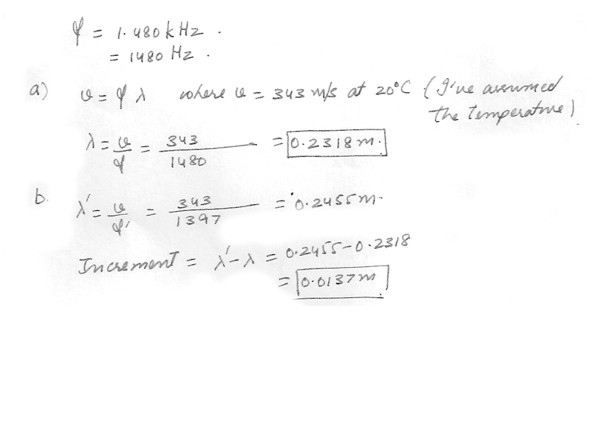
Physics Waves And Oscillations Level: High School
Vibration of a String
One of the 63.5 cm-long strings of an ordinary guitar is turned to produce the note B3 (frequency 245 Hz) when vibrating in its fundamental mode .A) Find the speed of transverse wave on this string . B) If the tension in this string is increased by 1.0% , what will be the new fundamental frequency of the string ?
C) If the speed of sound in the surrounding air is 344 m/s , find the frequency of the sound wave produced in the air by the vibration of the B3 string .
D) If the speed of sound in the surrounding air is 344 m/s , find the wavelength of the sound wave produced in the air by the vibration of the B3 string .

Physics Waves And Oscillations Level: High School
Vibration of a String
The portion of a cello string between the bridge and upper end of the finger board (that part of the string that is free to vibrate) is of length 60.0 cm , and this length of the string has mass 2.00 g . The string sounds and A2 note (440 Hz) when played .A) Where must the cellist put a finger (what distance x from bridge ) to play a D5 note (587 Hz) ? (see the figure at “click here”) . For both the At and D3 notes , the string vibrates in its fundamental mode .

Physics Waves And Oscillations Level: High School
Traveling Wave
A thin , taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation y(x,t) = (5.60 cm)sin (0.0340/cm)x] sin[(50.0 rad/s)t] , where the origin is at the left end of the string , the x-axis is along the string and the y-axis is perpendicular to the string .A) Find the amplitude of the two traveling waves that make up this standing wave .
B) What is the length of the string ?
C) Find the wavelength of the traveling waves.
D) Find the frequency of the traveling waves.
E) Find the period of the traveling waves.
F) Find the speed of the traveling waves.
G) Find the maximum transverse speed of a point on the string.

Physics Waves And Oscillations Level: High School
Traveling Wave
A fellow student of mathematical bent tells you that the wave function of a traveling wave on a thin rope is y(x,t) =Acos(k)x+(w)^2 . Being more practical minded , you measure the rope to have a length of L and a mass of m .A) Determine the amplitude
B) Determine the frequency
C) Determine the wavelength
D) Determine the wave speed
E) Determine the direction the wave is traveling
F) Determine the tension in the rope
G) Determine the average power transmitted by the wave

Physics Waves And Oscillations Level: High School
Normal Modes and Resonance Frequencies
A normal mode of a closed system is an oscillation of the system in which all parts oscillate at a single frequency . In general there are an infinite number of such modes . each one with a distinctive frequency f1 and associated pattern of oscillation .Consider an example of a system with normal modes : a string of length L held fixed at both ends , located at x =0 and x =L . Assume that waves on this system propagate with speed v . The string extends in the x direction ,and waves are transverse with displacement along the y direction .A) The string described in the problem introduction is oscillating in one of its normal modes . Which one of the following statement about the wave string is correct ?
a) The wave is traveling in the +x direction
b) The wave is traveling in the –X direction
c) The wave will satisfy the given boundary conditions for any arbitrary wavelength
d) The wavelength have only certain specific values if the boundary conditions are to be satisfied .
B) which of the following statement are true .
a) The system can resonate at only certain resonance frequencies f1 and the wavelength lamda 1 must be such that y1(0,1)=y1(L;t) = 0
b) A1 must be chosen so that wave fits exactly on the string.
C)Find the wavelengths(call them lamda 1,2,3) that ‘fit’ on the string , that is , those that satisfy the boundary conditions at x = 0 and x = L . These longest wavelengths have the lowest frequencies .
D)The frequency of each normal mode depends on the special part of wave function, which is characterized by its wavelength lamda 1 . Find the frequency f1 of the normal mode

Physics Waves And Oscillations Level: High School
Consider a traveling wave described by the formula y1 (x,t)= A sin (kx-wt) . This function might represents the lateral displacement of a string . a local electric field , the position of the surface of a body of water , or any of number of other physical manifestations of waves .A) Which one of the following statements about the wave described in the problem introduction is correct ?
a) The wave is traveling in the +x direction .
b) The wave is traveling in the –x direction .
c) The wave is oscillating but not traveling.
d) The wave is traveling but not oscillating .
B) Which of the expression given is a mathematical expression for a wave of the same amplitude that is traveling in the opposite direction ? At time t =0 this new wave should have the same displacement as yi (x,y) , the wave described in the problem introduction .
a) A cos (kx = wt )
b) A cos (kx + wt)
c) A sin (kx – wt)
d) A sin (kx + wt)
C) Find ye(x) and yt(t) . Keep in mind that yt(t) should be a trigonometric function of unit amplitude .
D) Which one of the following statement about the superposition wave
a) The wave is traveling in the +x direction
b) The wave is traveling in the _+ x direction
c) The wave is oscillating but not traveling
d) The wave is traveling but not oscillating

Physics Waves And Oscillations Level: High School
After landing on an unfamiliar planet , a space explorer constructs a simple pendulum of length L . She finds that the pendulum makes N complete swings in a time of t .A) What is the value of the g on the planet ?

Physics Waves And Oscillations Level: High School
You are watching an object that is moving is SHM . When the object is displaced 0.600 m to the right of its equilibrium position , it has a velocity of 2.20 m/s to the right and an acceleration of 8.40 m/s^2 to the left .A) How much farther from this point will the object move before it stops momentarily and then starts to move back to the left ?

Physics Waves And Oscillations Level: High School
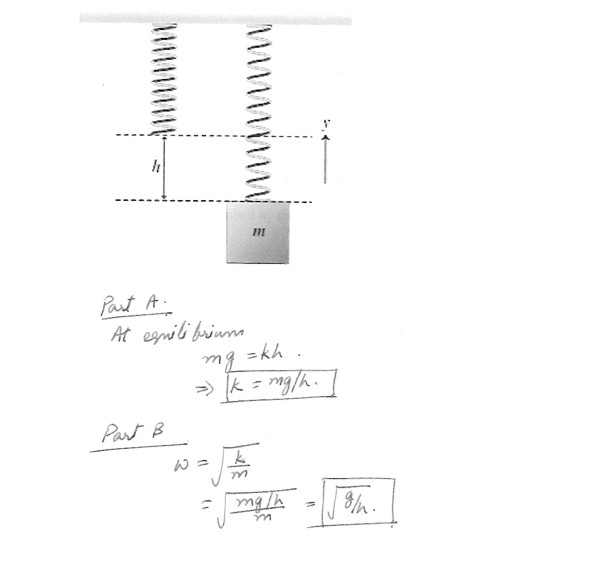
Vertical Mass and Spring Oscillator
A block of mass m is attached to the end of an ideal spring . Due to the weight of the block , the block remains at rest when the spring is stretched a distance h from its equilibrium length . The spring has an unknown spring constant k .A) What is the spring constant ?
B) Suppose that the block gets bumped and undergoes a small vertical displacement . Find the resulting angular frequency w of the block’s oscillation about its equilibrium position .
Physics Waves And Oscillations Level: High School
Simple Harmonic Motion
A block of mass m is attached to a spring whose spring constant is k . The other end of the spring is fixed so that when the spring is unstretched , the mass is located at x = 0 . Assume that the +x direction is to the right . The mass is now pulled to the right a distance beyond the equilibrium position and released , at time t = 0 , with zero initial velocity .A) At what time t1 does the block come back to its original position for the first time ?
B) Find the velocity v of the block as a function of time .
C)
D) Find the acceleration a of the block as a function of time .
E) Specify when the magnitude of the acceleration of the block reaches its maximum value .
F) Find the kinetic energy K of the block as a function of time .
G) Find K max , the maximum kinetic energy of the block
H) The kinetic energy of the block reaches its maximum when which of the following occurs ?
a) The displacement of the block is zero .
b) The displacement of the block is A
c) The acceleration of the block is at a maximum
d) The velocity of the block is zero .

Physics Waves And Oscillations Level: High School
Doppler Effect
The frequency of a steam train whistle as it approaches you is 530 Hz . After it passes you , its frequency is measured as 490 Hz. How fast was the train moving (assume constant velocity ) ?
Physics Waves And Oscillations Level: High School
Interference
Two loudspeakers are 2.40 m apart . A person stands 3.10 m from one speaker and 3.66 m from the other . What is the lowest frequency at which destructive interference will occur at this point ?a) Calculate the next highest frequency that also results in destructive interference at this point .

Physics Waves And Oscillations Level: High School
Beats
A piano tuner hears one beat every 2.00 s when trying to adjust two strings , one of which is sounding 421 Hz ,so that they sound the same tone . How far off in frequency is the other string ?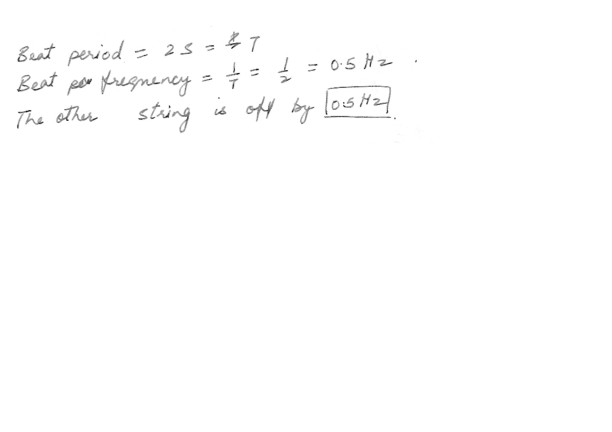
Physics Waves And Oscillations Level: High School
Standing Wave
Determine the length of an open organ pipe that emits middle C (262 Hz) when the temperature is 20.3 degreeC .