Physics Rotational Mechanics Level: High School
Moment of Inertia
Consider a rigid body consisting of two point masses , m1 and m2 , on the ends of the rod length L and negligible mass . Calculate the distance from each mass to the centre of mass , r1 and r2 . Show that the moment of inertia with respect to a rotation axis through the centre of mass and perpendicular to the rod is I = u L^2 ,where u is the reduced mass of the system , u = (1/m1 + 1 / m)^2 .
Physics Rotational Mechanics Level: High School
Moment of Inertia
The moment of inertia of mass about its rotation axis (the so-called “polar moment of inertia “ ) I , has been measured and found to be : I = 0.365 MR^2 , where T is the radius of the planet ,which we will assume to be spherical and M is the planet’s mass . Let’s try a two layer model of Mars , consisting of an iron core of radium r < R and density pc = 7.9 x 10^3 kg / m^3 . surrounded by a rocky mantel of density pm = 3.2 x 10^3 kg/ m^3 . Find an expression for “I/ (MR^2) as a function of r / R . You will have to express the mass M of the planet in terms of pc and pm .
Physics Rotational Mechanics Level: High School
Conservation of Energy
A uniformly thin vertical rod of mass M = 12.50 kg and length L = 2.250 is attached to a horizontal ceiling by a frictionless pivot at one end of the rod . The rod is initially displaced through an angle measured with respect to the vertical of x = 25.00 degrees . Use work energy considerations to determine the following .a) The angular speed of the rod at the instant it is vertical
b) Determine the angular momentum and the rotational kinetic energy of the rod at the instant it is vertical .

Physics Work,Power & Energy Level: High School
Vertical Loop
The maximum acceleration a human can stand is about 7.0 g . What is the minimum radius of curvature that a jet plane’s pilot pulling out of a vertical dive can tolerate at a speed of 250 m / s ?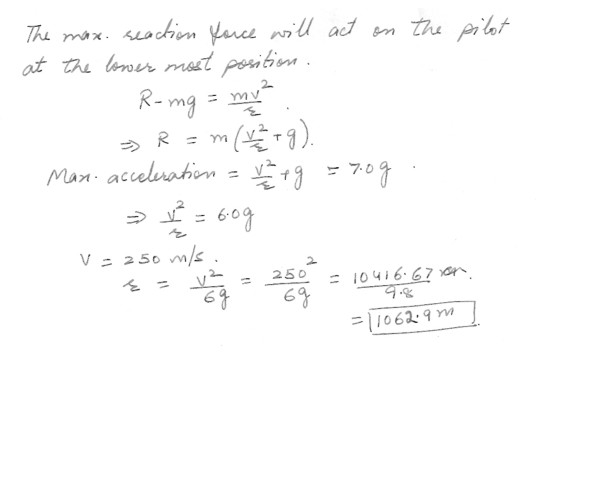
Physics Gravitation Level: High School
A satellite of Jupiter has an orbital period of 1.77 days and orbital radius of 4.22 x 10 5 km . From these data , determine the mass of Jupiter ? (that’s 4.22 x ten to the fifth power )
Physics Rotational Mechanics Level: High School
A 50 kg child stands at the rim at the of a merry-go-round of radius 2.00 m , rotating with an angular speed of 3.00 rad / s ,
a) What is the child centripetal acceleration ?
b) What is the minimum force between his feet and the floor of the carousel that is required to keep him in the circular path ?
c) What minimum coefficient of static friction is required ? Is the child likely to stay on the merry-go-round ?

Physics Rotational Mechanics Level: High School
a) What is the tangential acceleration of a bug on the rim of a 10-in. – diameter disk if the disk move from rest to an angular speed of 78 rev / min in 3.0 s ?
b) When the disk is at its final speed , what is the tangential velocity of the bug ?
c) One second after the bug starts from rest , what are its tangential acceleration , centripetal acceleration and total acceleration ?

Physics Rotational Mechanics Level: High School
A merry-go-round (MGR) of mass 200.0 kg and radius 3.0 m is initially stationary . Two children , each of mass 40.0 kg , run from opposite directions at 4 m/s and grab onto opposite positions on the MGR , calculate the final angular velocity of the MGR with the children on it . Treat MGR as a uniform disk . (Hint : the angular momentum of a point mass about a point is given by L = m , V tangential. r . This can be seen from the basic formula L = Iw by substituting I = mr^2 and w = v tangential / r )
Physics Rotational Mechanics Level: High School
A mass of 1000.0 kg is suspended by a rope wound around an axle of radius 0.1 m . The axle is mounted on frictionless bearings and attached to a disk flywheel . The flywheel has a radius of 1.000 m and mass of 20 kg . The axle has negligible mass and negligible moment of inertia .a) Calculate the acceleration of the 1000 kg mass .
b) Calculate the tension in the rope .

Physics Rotational Mechanics Level: High School
Rotational Equilibrium
A horizontal beam of mass 100.0 kg and length 6.0 m is hinged at the wall and hold by a cable at 45 deg . A load of mass 1000.0 kg is hung from the beam . Calculate the tension in the cable for each of the 4 indicated positions (From left to right – 0m, 2m , 4m , 6m . Present the results in a table . There is only one load , you are analyzing 4 different positions .
Physics Work,Power & Energy Level: High School
Conservation of Linear Momentum
A truck of mass 3000 kg traveling due east collides with a car of mass 1500 kg traveling due north . The two stick together and skid at an angle 45.0 deg north of east for a distance of 20.0 m . The coefficient of friction Mk = 1.000 . Calculate the speed of each vehicle before the collision .
Physics Gravitation Level: High School
It is proposed to put the moon into a 31-day orbit , to prevent there from being 2 full moons in a month . Currently the moon orbits at r = 3.831 x 10^8 m with KE = 3.832 x 10^28 J and PE = 7.664 x 10^28 J . Using the equation PE = -G ME. m/r . and remembering that PE is always negative in this convention .a) Calculate the new orbital distance .
b) Calculate the new PE , KE and the amount of energy necessary to make this change .

Physics Rotational Mechanics Level: High School
Centripetal Acceleration
At amusement parks , there is a popular ride where the floor of a rotating cylindrical room falls away , leaving the backs of the riders “plastered” against the wall . Suppose the radius of the room is 3.40 m and the speed of the wall is 11.2 m / s . When the floor falls away .a) What is the force of the centripetal force acting on the riders ? The gravitational force , the cavitron force between the rider and the wall , or the normal force exerted on the rider by the wall ?
b) How much centripetal force acts on a 55.0 kg rider ?
c) What is the minimum coefficient of static friction that must exist between the rider’s back and the wall , if the rider is to remain in place when the floor drops away ?

Physics Rotational Mechanics Level: High School
The earth rotates once per day about an axis passing through the north and south poles , an axis that is perpendicular to the plane of the equator , Assuming the earth is a sphere with a radius of 6.38 x 10^6 m . Determine the speed and centripetal acceleration of a person situated at each of the following .a) the equator .
b) a latitude of 54.0 degree north of the equator .

Physics Work,Power & Energy Level: High School
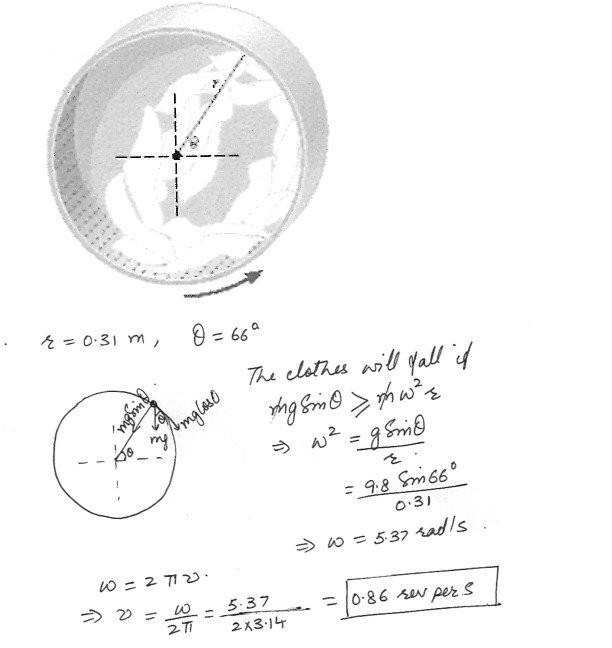
Vertical Circle , Centrifugal Force
In an atomic clothe drier , a hollow cylinder moves the clothe on a vertical circle (radius r = 0.31 m ) , as the drawing shows at “click here” . The appliance is designed so that the clothes tumble gently as the dry . This means that when a piece of clothing reaches an angle of theta above the horizontal , it loses contact with the wall cylinder and falls onto the clothes below . How many revolutions per second should the cylinder make in order that the clothes lose contact with the wall when theta = 66.0 degree ?